Abstracts of presentations, mostly from:

• Association for Research in Vision and Opthalmology (ARVO)
  
• Vision Sciences Society (VSS)
  
• Society for Neuroscience (SFN)
  
• Computational and Systems Neuroscience (COSYNE)
  
• European Conference on Visual Perception (ECVP)

In area MT, responses to visual motion can be characterized by comparing responses to simple grating stimuli with responses to compound stimuli (plaids) made by adding two gratings. Component direction selective (CDS) cells responses to plaids can be predicted from the sum of the individual stimulus components, while pattern direction selective (PDS) cells responses reflect a nonlinear computation of pattern motion direction independent of the orientation of the individual stimulus components. In MT, about half the cells are CDS, a sizeable minority is PDS, and others seem to have intermediate properties. To distinguish the computation of PDS and CDS cells, we decided to reexamine this issue using the simplest plausible model we could devise.

We presented continuous sequences of compound gratings with multiple components that differed in direction, speed, and/or spatial frequency (hyperplaids). We used the resulting MT unit activity to estimate a simple model in which responses are given by linear combination of directionally-selective inputs preferring different directions and speeds, followed by half-rectification. For both CDS and PDS cells, this simple model predicted the responses to both grating, plaid, and hyperplaid stimuli with surprising accuracy, suggesting that CDS and PDS cells differ not in computational style but in parametric detail. Most cells had excitatory inputs near the preferred direction, balanced by a suppressive input from other directions, especially those near 180 deg from the preferred. This motion opponency was much stronger in PDS cells than in CDS cells, and the breadth of excitation in PDS cells was also usually greater than CDS cells. Taken together, these two factors account well for the distinction between the responses of PDS and CDS cells. Moreover, the continuous nature of their variation offers a natural explanation for the continuum of response patterns seen in MT.

Correlated spiking activity in nearby neurons is a common feature of neural circuits. We show that a generalized linear model can be used to account for the correlation structure in the spike responses of a group of nearby neurons in primate retina. The model consists of: (1) a linear receptive field that operates on the stimulus; (2) a linear filter that captures the effects of the neuron's own spike history; (3) a set of linear filters that capture the effects of spiking in neighboring cells; and (4) an output nonlinearity that converts the total input to an instantaneous probability of spiking. The model is closely related to the more biophysically realistic integrate-and-fire model, and can exhibit a wide array of biologically relevant dynamical behaviors, such as refractoriness, spike rate adaptation, and bursting. It has previously been used to characterize the isolated responses of individual neurons.

We have applied the model to simultaneously-recorded responses of groups of macaque ON and OFF parasol retinal ganglion cells, stimulated with a 120-Hz spatiotemporal binary white noise stimulus. We find that the model accurately describes the stimulus-driven response (PSTH), and reproduces both the autocorrelations and pairwise cross-correlations of multi-cell responses. Moreover, by examining the contribution of stimulus and spike train dependent inputs, the model allows us to reliably predict the relative significance of signal and noise-dependent correlations, which we verify by examining responses to a repeated stimulus. Finally, we show that the model can be used to map functional connectivity, providing a complete description of the identity, direction and form of functionally significant connections between cells.

The perceived visual speed of a translating spatial intensity pattern varies as a function of stimulus contrast, and is qualitatively consistent with that predicted by an optimal Bayesian estimator based on a Gaussian prior probability distribution that favors slow speeds (Weiss, Simoncelli & Adelson, 2002). In order to validate and further refine this hypothesis, we have developed a more general version of the model. Specifically, we assume the estimator computes velocity from internal measurements corrupted by internal noise whose variance can depend on both stimulus speed and contrast. Furthermore, we allow the prior probability distribution over speed to take on an arbitrary shape. Using classical signal detection theory, we derive a direct relationship between the model parameters (the noise variance, and the shape of the prior) and single trial data obtained in a two-alternative forced choice speed-discrimination task. We have collected psychophysical data, in which subjects were asked to compare the apparent speeds of paired patches of drifting gratings differing in contrast and/or speed. The experiments were performed over a large range of perceptually relevant contrast and speed values. Local parametric fits to the data reveal that the likelihood function is well approximated by a Normal distribution in the log speed domain, with a variance that depends only on contrast. The prior distribution on speed that best accounts for the data shows significantly heavier tails than a Gaussian, and can be well approximated across all subjects by a power-law function with an exponent of 1.4. We describe a potential neural implementation of this model that matches the derived forms of the likelihood and prior functions.

Slides from talk
Short article: SPIE-04

Given two quantitative models for the perceptual discriminability of stimuli that differ in some attribute, how can we determine which model is better? A direct method is to compare the model predictions with subjective evaluations over a large number of pre-selected examples from the stimulus space, choosing the model that best accounts for the subjective data. Not only is this a time-consuming and expensive endeavor, but for stimulus spaces of very high dimensionality (e.g., the pixels of visual images), it is impossible to make enough measurements to adequately cover the space (a problem commonly known as the "curse of dimensionality").

Here we describe a methodology, Maximum Differentiation Competition, for efficient comparison of two such models. Instead of being pre-selected, the stimuli are synthesized to optimally distinguish the models. We first synthesize a pair of stimuli that maximize/minimize one model while holding the other fixed. We then repeat this procedure, but with the roles of the two models reversed. Subjective testing on pairs of such synthesized stimuli provides a strong indication of the relative strengths and weaknesses of the two models. Specifically, if a pair of stimuli with one model fixed but the other maximized/minimized are very different in terms of subjective discriminability, then the first (fixed) model must be failing to capture some important aspect of discriminability that is captured by the second model. Careful study of the stimuli may, in turn, suggest potential ways to improve a model or to combine aspects of multiple models.

To demonstrate the idea, we apply the methodology to several perceptual image quality measures. A constrained gradient ascent/descent algorithm is used to search for the optimal stimuli in the space of all images. We also demonstrate how these synthesized stimuli lead us to improve an existing model: the structural similarity index [Wang, Bovik, Sheikh, Simoncelli, IEEE Trans Im Proc 13(4), 2004].

Cells in MT are tuned for the direction of moving stimuli. In response to a superimposed pair of sinusoidal gratings (a plaid), component direction selective cells (CDS) respond in a manner predicted by summation of their responses to the constituent grating stimuli. In contrast, pattern direction selective cells (PDS), are tuned for the two-dimensional velocity corresponding to a rigid displacement of the plaid, consistent with the way we perceive these stimuli. To investigate the computation of pattern direction, we used a spike-triggered analysis to characterize the responses of individual MT neurons in terms of a linear weighting of signals elicited by sinusoidal gratings moving at different directions and speeds. On each trial, each of a large set of gratings was assigned a random phase and one of three contrasts: 0, C/2, or C. We recovered a linear weight for each stimulus dimension by computing the mean contrast of each grating before a spike (the spike-triggered average or STA). The arrangement of the positive and negative weights of the STA predicted whether the cell responded with pattern or component selectivity. Specifically, strong, broadly tuned inhibition in PDS cells suppressed responses to the individual plaid components, resulting in tuning for the direction of plaid motion. In CDS cells, such suppression was weak or absent. These results, which are consistent with the predictions of Simoncelli & Heeger (Vis. Res., 1998), suggest that broadly tuned null direction suppression (motion opponency) plays a fundamental role in computing pattern motion direction in MT.

There is increasing experimental evidence that a wide range of psychophysical results can be successfully explained using Bayesian observer models. While the Bayesian observer model seems to provide an accurate statistical description on the behavioral level, the neural instantiation of such an inference process is unclear. In particular, it is an open question as to whether the brain needs an explicit representation of probability distributions in order to perform Bayesian inference. A variety of neural strategies for implementing inference processes have been proposed (e.g., Pouget, Dayan and Zemel, 2003; Rao, 2004) but only little work has been done to explicitly test them against both psychophysical and physiological data of a particular perceptual task.

In order to address this question we focus on implementation strategies for visual speed perception. The observed contrast dependence of speed perception is in good agreement with a Bayesian observer model that incorporates a statistical prior that visual motion on the retina tends to be slow (Simoncelli 1993; Weiss etal. 2002). We have recently estimated the shapes of the prior on speed and the contrast-dependent likelihood using 2AFC psychophysical speed discrimination experiments (Stocker and Simoncelli, NIPS*04). There is also a wealth of physiological data available from the Medial Temporal (MT) area in monkeys, which is considered to be central for visual motion processing. Assuming that monkey neural responses provide a qualitatively reasonable approximation to their human counterparts, these data allow us to constrain neural implementations and potentially to predict neural response characteristics based on known psychophysics.

We find that all strategies based on an explicit representation of the likelihood function through the population activity of MT neurons seem implausible for implementing a Bayesian motion perception solution. In the Bayesian solution, the likelihood width needs to increase with decreasing stimulus contrast. However, the physiological literature suggests that MT tuning curves do not change with decreasing contrast. This physiological finding also imposes constraints on the implementation of the prior. It rules out strategies that propose a preferred sampling or weighting of low-speed tuned cells, because they also would require a broadening of the tuning curves to account for the perceptual shift. On the other hand, a prior that is explicitly expressed by the responses of a given population of neurons - which has been proposed in other context (Yu and Dayan, 2005) - requires stable and continuous firing rates of those neurons. This seems implausible for a perceptual prior that presumably changes slowly (because of its metabolic costs), and does not appear to be supported by any physiological evidence.

As an alternative, we suggest a different implementation that avoids the explicit representation of likelihood and prior in a population of neurons. The likelihood is implicitly represented, given that the population response of MT cells represents the unbiased measurement and assuming independent Poisson spiking statistics in which the spike rate variance is proportional to the rate. In this way, the likelihood function for a given population response does broaden with decreasing contrast yet the population response remains in complete agreement with known physiology. As for the prior, there are several possibilities of implementation. One is that the prior is imposed by a contrast response function that is non-uniform across different cells, depending on their preferred speed tuning. For example, if the firing rate of cells tuned for low speeds decreases less with decreasing contrast than those tuned for higher speeds, the population mean would shift increasingly towards slower speeds with decreasing contrast. Another possibility is that the prior is imposed by a read-out mechanism that performs a biased normalization of the responses that depends on the preferred speed tuning and the response amplitude. These are testable hypotheses, and we are currently exploring physiological data sets to evaluate their plausibility.

The present study, in combination with previously derived psychophysical and physiological data, indicates that an explicit implementation of the likelihood function and the prior distribution in the primate visual motion area MT seems unlikely, and is not necessary to perform Bayesian inference.

Much recent work has focused on the significance of correlated firing in the responses of groups of neurons. Here we explore the use of advanced statistical characterization methods to build realistic models which account for such correlations. We examine two models, a generalized integrate-and-fire (IF) model, and a generalized linear model (GLM), which have so far been applied to characterize the complete input-output characteristics of individual neurons. We show how these models can be reliably fit to the responses of pairs of neurons, and use them to examine functional dependencies between neurons. We find that many of the observed correlations in the spike trains of neuronal pairs can be accounted for by these models. Finally we sketch an idea for using these models to explore the coding significance of correlated firing.

The two models define the spike train emitted by a neuron as the result of a two-stage process: an initial linear filtering stage, which governs the membrane potential, followed by a nonlinear spike generation mechanism. The initial linear stage consists of three filters: (1) a stimulus filter, or linear receptive field, which captures the effects of the stimulus, (2) a spike-history filter, which captures the influence of past spikes (e.g., the refractory period), and (3) a cross-neuron filter, which captures the effects of spikes in other neurons on the response. This architecture captures both stimulus-dependent and noise-dependent correlations between neurons. Stimulus-dependent correlations arise from overlap in individual stimulus filters, whereas noise-dependent correlations arise from the cross-neuron filters. The spike-history filter captures a wide array of biologically relevant dynamical behaviors of individual neurons, such as spike rate adaptation, facilitation, bursting, and bistability.

The primary difference between the models arises in the nonlinear, probabilistic spiking stage. In the IF model, spikes occur whenever voltage crosses a fixed threshold, after which voltage resets instantaneously to zero, and response variability results from an injected Gaussian white noise current. In the GLM model, voltage is converted to an instantaneous probability of spiking via a fixed, accelerating nonlinear function [see also Truccolo et al, 2004]. This model can be considered an approximation to integrate-and-fire, where instead of spiking at a fixed threshold, the probability of spiking increases exponentially as a function of voltage. We have shown in recent work [Pillow et al, NIPS 2003; Paninski et al, Neural Comp 2004; Paninski, Network 2004] that these models can be tractably and efficiently fit to data using maximum likelihood estimation. Specifically, the log-likelihood functions of the models are concave, meaning that gradient ascent techniques can be used to efficiently find the optimal estimate of the model parameters (i.e. filters, and the reversal and conductance parameters for the IF model). The technique extends straightforwardly to multi-cell data.

We apply these models to probe the origin of correlations in simultaneously-recorded responses of pairs of macaque retinal ganglion cells, stimulated with a 120-Hz spatially and chromatically varying binary white noise stimulus (i.e. spatial and chromatic flicker). We show that the IF and GLM models reproduce the detailed individual spike train statistics, as well as correlations between spike trains of different cells. We analyze the relative contribution of signal and noise to correlated firing by comparing the performance of the model fit with and without the cross-neuron input. We find that in some cell pairs, the models predict nearly uncorrelated responses without cross-neuron input, but a substantial correlation in spike trains with cross-neuron terms present. We provide a detailed comparison of the performance of the two models and a discussion of how they can be used to investigate the coding significance of correlated firing.

A neural encoding model provides a mathematical description of the input-output relationships between high-dimensional sensory inputs and spike train outputs. We consider two fundamental criteria for evaluating such models: the power of the model to accurately capture spiking behavior under diverse stimulus conditions, and the efficiency and reliability of methods for fitting the model to neural data. Both of these are essential if the model is to be used to answer questions about neural encoding of sensory information.

Based on these criteria, we compare three recent models from the literature. Each includes a linear filter that determines the influence of the stimulus (i.e., a receptive field), followed by a nonlinear, probabilistic spike generation stage which determines the influence of spike-train history. This history-dependence allows the models to exhibit many of the non-Poisson spiking behaviors observed in real neurons such as refractoriness, adaptation, and facilitation. All three models allow one to compute the probability of spiking conditional on the recent stimulus and spike history. Finally, all three models can be tractably fit to extracellular data (i.e. the stimulus and a list of recorded spike times) by ascending the likelihood function.

The first model is a generalized integrate-and-fire (IF) model (e.g. Keat et al, Neuron, 2001; Jolivet et al., J. Neurophys. 2004). It consists of a leaky IF compartment, driven by a stimulus-dependent current and a spike-history dependent current, and a Gaussian noise current. The first two currents result from a linear filtering of the stimulus and spike train history, respectively, and membrane conductance can also take on a linear dependence on the input. We have shown recently that the parameters of this model -- the stimulus and spike-history filters, and the reversal, threshold, and conductance parameters -- can be robustly and efficiently fit using straightforward ascent procedures to compute the maximum likelihood solution, because the loglikelihood is guaranteed to be concave (Pillow et al, NIPS 2003; Paninski et al., Neural Comp., 2004). Although the likelihood computation is computationally intensive, the model has a clear and well-motivated biological interpretation, and has been found to account for an variety of neural response behaviors (Paninski et al., Neurocomputing, 2004; Pillow et al., submitted);

The second model is a generalized linear model (GLM) (see also, e.g., Truccolo et al., J. Neurophys. 2004), which resembles the IF model, except that the spiking is determined by an instantaneous nonlinear function of membrane voltage. This can be considered an "escape-rate" approximation to integrate-and-fire, where instead of spiking at a fixed threshold, the spike probability is a sharply accelerating function of membrane potential. Like the IF model, this model has a concave log-likelihood function, guaranteeing the tractability of maximum likelihood estimation. Moreover, the likelihood function for this model is much simpler to compute (Poisson likelihoods, instead of crossing-time probabilities of Gaussian processes), so fitting is much faster and easier to implement than for the IF model (though see Paninski et al., this meeting, for recent improvements on computing the IF likelihood). One drawback is that no similar concavity guarantees exist for the conductance parameters for this model, meaning that the model may be less flexible for modeling the responses of some neurons in which post-spike conductance changes play an important role.

Finally, we examine a model popularized by Berry and Meister (J. Neurosci. 1998; see also Miller and Mark, JASA 1992). Unlike the IF and GLM models, where spike history interacts additively with the stimulus input, this model decomposes the probability of spiking into the product of a "free firing rate," which depends only on the stimulus, and a "recovery function" which depends only on the time since the last spike. Berry and Meister proposed some simple techniques for estimating the two model components. We have recently developed a maximum likelihood method that is more efficient and provides accurate estimates under more general conditions. Specifically, optimization of the post-spike "recovery" function (to maximmize the likelihood of the data) may be performed uniquely and analytically, leading to a highly efficient estimator (Paninski, Network: Comp. Neur. Sys., 2004). As such, this model is the most efficient of the three in terms of estimation of the recovery function; however, while the loglikelihood is concave as a function of the post-spike term and stimulus-dependent term individually, we have no guarantees on the joint concavity of this likelihood, and so in principle some local maxima might exist when simultaneously optimizing both terms. More importantly, the dependence on spike-train history is captured entirely by the time since the last spike, which limits the model's ability to reproduce more complicated spiking dynamics (e.g., slow adaptation) that can be captured by either of the other two models.

We provide a detailed comparison of all three models, with a careful examination of their performance capturing the input-output characteristics and spike-train history effects in the responses of real neurons. We examine both the accuracy with which they predict responses to novel stimuli, and their residual error in predicting the distribution of interspike intervals, which can be quantified using a version of the time-rescaling theorem applied to each model.

Models used to characterize visual neurons typically involve unrealistic assumptions that fail to describe important aspects of spiking statistics. We investigated the ability of a cascade model with stochastic integrate-and-fire (IF) spiking to account for the light responses of primate retinal ganglion cells (RGCs). In the model, an initial linear filtering of the stimulus (the temporal receptive field) drives a noisy, leaky IF spike generator. An after-current is injected into the integrator after each spike, enabling the model to capture a wide range of realistic spiking statistics. This model provides a reasonable approximation to the biophysics of spike generation, and can be reliably and efficiently fit to extracellular spike time data. Here we show that the model is capable of characterizing the stimulus-dependence, timing and intrinsic variability of RGC light responses.

Multi-electrode extracellular recordings from primate RGCs were obtained from isolated retinas stimulated with spatially uniform temporal white noise (flicker). The stochastic IF model was fit to recorded spike times using maximum likelihood, and was subsequently used to predict RGC responses to multiple repeats of a novel stimulus. The model provided a more accurate description of spike rate, count variability, and timing precision of RGC responses than a commonly-used Linear-Nonlinear-Poisson cascade model. Because the model approximates a biophysical description of RGC spike generation, it provides an intuition about the origins and stimulus dependence of spike timing variability: voltage noise in a leaky integrator driven across threshold.

V1 neurons are commonly classed as simple and complex based upon their responses to drifting sinusoidal gratings. The periodic response of a simple cell is typically modeled using a single linear filter followed by a half-squaring nonlinearity. Phase-insensitivity in complex cells arises in the motion-energy model by squaring the output of two linear filters in quadrature. In fact, one observes a continuum of response patterns to sinusoidal gratings in V1 cells. We performed a spike-triggered characterization of macaque V1 cells with a range of phase-sensitivities to estimate the number and type of linear filters involved in the generation of these cell s responses.

We stimulated neurons with a dense, random, binary bar stimulus con- fined to the classical receptive field. For each cell, we recovered a set of linear filters describing the generation of the neuron s response by calculating the spike-triggered average (STA) and significant axes revealed by applying a principal components analysis to the spike-triggered covariance matrix (STC). Assuming a linear-nonlinear-poisson (LNP) model, the number of recovered filters in this analysis sets a lower bound on the number of filters the cell uses in performing its computations.

The results revealed by this analysis predict the continuum of modulation in response to gratings across the population of V1 neurons. In simple cells we recovered an STA with clear spatio-temporal structure in addition to at least one additional filter. The additional filter tended to differ from the STA by a phase shift and decreased the modulation of the cell s response. However, in the more modulated simple cells, the weight of this filter was weak relative to the STA and thus had only a small effect on response. For less modulated simple cells, the weight of this additional filter increased. For complex cells, the STA weakened and two full-rectified, quaderature phase filters were revealed by the STC, as predicted by the energy model.

In complex cells, our analysis often recovered more than one filter pair. While the first pair of filters always had clear spatio-temporal structure in the middle of the receptive field, additional filter pairs tended to have more structure near the receptive field s edges. These additional pairs thus describe the spatio-temporal tuning along the receptive field fringe. These filters were not the product of eye movements, deviations from Poisson spiking, or the particular stimulus used for the characterization. In the context of the LNP model, the presence of additional filter pairs beyond the first suggests the existence of multiple spatially-shifted subunits in complex cells.

Light responses of retinal ganglion cells (RGCs) exhibit several kinds of nonlinearity. These nonlinearities have usually been probed with restricted sets of stimuli that do not provide a complete characterization of (a) the spatial and temporal structure of the nonlinearities and (b) neural response as a function of the stimulus. We developed a spike-triggered covariance (STC) analysis to provide such a characterization of primate RGC light responses.

Multi-electrode recordings from macaque RGCs were obtained from isolated retinas stimulated with one-dimensional spatiotemporal white noise (i.e. flickering bars). Spike-triggered average (STA) analysis revealed center-surround spatial organization and biphasic temporal integration expected from RGCs. Eigenvector analysis of the STC revealed components with spatial and temporal structure distinct from the STA. Excitatory STC components exhibited temporal structure similar to the STA, but finer spatial structure, consistent with input from multiple spatial subunits combined nonlinearly. Suppressive STC components exhibited spatial structure similar to the STA or to excitatory STC components, but temporal structure that was time-delayed relative to the STA, consistent with spike generation or contrast gain control nonlinearities.

A model consisting of spatially shifted subunits with a simple rectifying nonlinearity, summed and followed by leaky integrate-and-fire spike generation, accurately reproduced the observed STA, contrast-response function, and detailed spatial and temporal structure of STC components. These results suggest that spatial and temporal properties of nonlinearities in macaque RGC light response can be identified and characterized accurately using STC analysis.

Related pubs: CNS*03 article | Book chapter on neural characterization

In the macaque visual system, directional selectivity (DS) is first found in neurons in primary visual cortex, area V1. It remains unclear whether this selectivity arises purely from the integration of excitatory inputs with appropriately arranged spatiotemporal offsets, or if additional suppressive influences are also involved. To address this issue, we measured the responses of V1 neurons in opiate anaesthetized, paralyzed macaques to spatiotemporal binary noise stimuli, and applied a spike-triggered covariance analysis (STC) to the data. The analysis extracts a set of excitatory and suppressive linear components as well as the nonlinear rules by which they are combined. In some DS cells the STC was dominated by excitatory components, and a model based on these components accurately predicted the cells directionality as measured with gratings. For other DS neurons, STC revealed strong excitatory and suppressive components with opposite direction preferences. For these neurons, a model that included only excitatory components overestimated the response to gratings moving in the nonpreferred direction; incorporating suppressive components in the model yielded accurate predictions of selectivity. To further explore these suppressive influences, we constructed stimuli which systematically varied the contribution of the excitatory and suppressive components. Stimuli tailored to activate the excitatory components alone elicited vigorous responses. As predicted, these responses were substantially reduced by the presence of stimuli tailored to activate the suppressive components. These results suggest that V1 may implement a multistage computation in which directional selectivity is initially but imperfectly established by suitable spatiotemporal filters, and then refined by suppressive signals that eliminate unwanted responses to non-preferred stimuli.

Related pubs: CNS*02 article | Book chapter on neural characterization

A variety of models of stimulus-driven neural activity are of cascade form, in which a linear filter is followed by a nonlinear probabilistic spiking mechanism. One simple version of this model implements the nonlinear stage as a noisy, leaky, integrate-and-fire mechanism. This model is a more biophysically realistic alternative to models with Poisson (memory-less) spiking, and has been shown to be effective in reproducing various spiking statistics of neurons in vivo. However, the estimation of the full model parameters from extracellular spike train data has not been examined in depth.

We address this problem here in two steps. First, we show how the problem can be formulated in terms of maximum likelihood estimation, which provides a statistical setting and natural "cost function" for the problem. Second, we show that the computational problem of optimizing this cost function is tractable: we provide a proof that the likelihood function has a single global optimimum and introduce an algorithm that is guaranteed to find this optimum with reasonable efficiency. We demonstrate the effectiveness of our estimator with numerical simulations and apply the model to both in vitro and in vivo data.

In models of the response of V1 and MT cells, the gain control signal is taken to be the pooled activity of nearby cells of all direction and orientation preferences (Heeger, 1992; Simoncelli & Heeger, 1998), but the promiscuity of this inhibition has not been directly tested. We studied the stimulus specificity of this signal in MT cells by comparing responses to drifting test gratings presented alone with those measured in the presence of a drifting pedestal grating. Targets were presented at two equally effective locations within the receptive field, and could be either superimposed or separated.

When the pedestal grating drifted in the preferred direction of the cell, responses to the test gratings were strongly reduced by the pedestal, regardless of whether the test and pedestal were separated or superimposed. These results support previous work suggesting gain control acts globally over MT receptive fields (Britten & Heuer, 1999; Majaj et al, SFN 2000). When the pedestal grating drifted in the null direction, test responses were reduced only when the test grating was superimposed on the pedestal and were largely unaffected when the gratings were separated. The difference between the results obtained with masks moving in the preferred and null directions suggests that gain control in MT is tuned for the direction of motion.

Moreover, the existence of a tuned normalization signal in MT that follows an untuned normalization stage in V1 may describe the phenomenon of local motion opponency (Qian et al. 1994) without the need to invoke an explicit opponent computation.

Most neurons in macaque area MT (V5) respond vigorously to stimuli moving in a preferred direction, and are suppressed by motion in the opposite direction. The excitatory inputs come from specific groups of directionally selective neurons in lower-order areas, but the inhibitory signals are not so well understood. Some models (e.g. Simoncelli and Heeger, 1998, Vision Res) assume that these signals are pooled across the receptive field, but Qian et al. (1994, J Neurosci) suggested instead that inhibitory inputs interact with excitatory ones only within local regions of space. To explore the location and direction specificity of interactions between MT receptive field subregions, we stimulated small areas of the receptive field with Gabor patches drifting in the preferred direction. We presented these alone and in combination with stimuli drifting in non-preferred directions so that we could study inhibitory signals against background firing elevated by preferred stimuli. Non-preferred gratings suppressed responses strongly when they were presented in the same retinal location as the preferred grating. When the two gratings were separated, suppression was much reduced and was no larger than the suppression of spontaneous firing produced by a non-preferred stimulus presented alone. Our results show that non-preferred stimuli can only inhibit responses generated by excitatory stimuli from nearby regions of space; this suggests that direction-specific inhibition acts within spatially localized subregions of the receptive field. The results can be described by a model in which local excitation and inhibition are combined and rectified before a final stage of spatial pooling.

More recent: NIPS article | Book chapter

Spike-triggered average (reverse correlation) techniques are effective for linear characterization of neural responses. But cortical neurons exhibit striking nonlinear behaviors that are not captured by such analyses. Many of these nonlinear behaviors are consistent with a contrast gain control (divisive normalization) model. We develop a spike-triggered covariance method for recovering the parameters of such a model. We assume a specific form of normalization, in which spike rate is determined by the halfwave-rectified and squared response of a linear kernel divided by the weighted sum of squared responses of linear kernels at different positions, orientations, and spatial frequencies. The method proceeds in two steps. First, the linear kernel of the numerator is estimated using traditional spike-triggered averaging. Second, we measure responses with the excitation of the numerator kernel held constant (this is accomplished by stimulus design, or during data analysis) but with random excitation along all other axes. We construct a covariance matrix of the stimuli eliciting a spike, and perform a principal components decomposition of this matrix. The principal axes (eigenvectors) correspond to the directions in which the response of the neuron is modulated divisively. The variance along each axis (eigenvalue) is monotonically decreasing as a function of strength of suppression along that axis. The kernels and weights of an equivalent normalization model may be estimated from these eigenvalues and eigenvectors. We demonstrate through simulation that the technique yields a good estimate of the model parameters, and we examine accuracy as a function of the number of spikes. This method provides an opportunity to test a normalization model experimentally, by first estimating model parameters for an individual neuron, and then examining the ability of the resulting model to account for responses of that neuron to a variety of other stimuli.

More recent: Book chapter describing this work.

Purpose: In previous work, we have shown that an extended divisive normalization model, in which each neuron's activity is divided by a weighted sum of the activity of neighboring neurons, can be derived from natural image statistics (Simoncelli & Schwartz, ARVO-98). Here we examine whether continuous re-optimization of normalization parameters according to recent input statistics can account for adaptation in V1 simple cells. Methods: Images are decomposed using a fixed linear basis, consisting of functions at different scales, orientations, and positions. Normalized responses are computed by dividing the squared response of each neuron by a weighted sum of squared responses at neighboring positions, orientations, and scales, plus a constant. Both the weights and additive constant are optimized to maximize the statistical independence of the normalized responses for a given image ensemble. Specifically, a generic set of weights is computed from an ensemble of natural images, and is used to compute unadapted responses. An adapted set of weights is computed from an ensemble consisting of natural images mixed with adapting stimuli. Results: The changes in response resulting from use of the adapted normalization parameters are remarkably similar to those seen in adapted V1 neurons. Adaptation to a high-contrast grating at the optimal frequency causes the contrast response function to undergo both lateral and compressive shifts, as documented in physiological experiments (Albrecht et al., 1984). In addition, adaptation to a grating of non-optimal frequency or orientation produces suppression in the corresponding flank of the tuning curve. Thus, the model distinguishes between the effects of contrast and pattern adaptation. Conclusions: A divisive normalization model, with parameters optimized for the statistics of recent visual input, can account for V1 simple cell behavior under a variety of adaptation conditions.

More recent: nips*98 | Nature Neuroscience article.

Purpose: A number of authors have used normalization models to successfully fit steady-state response data of V1 simple cells. Rather than adjusting model parameters to fit such data, we have developed a normalization model whose parameters are fully specified by the statistics of an ensemble of natural images (Simoncelli & Schwartz, ARVO-98). We show that this model can account for suppression of V1 responses by stimuli presented in an annular region surrounding the classical receptive field. Methods: The stimulus is decomposed using a fixed set of linear receptive fields at different scales, orientations, and spatial positions. A model neuron's response is computed by squaring the linear response and dividing by the weighted sum of squared linear responses of neighboring neurons and an additive constant. Both the normalization weights and the constant are optimized to maximize the statistical independence of responses over an ensemble of natural images. In addition, we examine the variability in model neuron responses when these parameters are optimized for individual images. Results: The simulations are consistent with electro-physiological data obtained in two laboratories (Cavanaugh et al. 1998, Müller at al. 1998). In particular, the model responses match the steady state responses of the neuron as a function of orientation, spatial frequency and proximity of the surround. Moreover, the variability of suppression strength when the model parameters are optimized for individual images is no greater than the variability of the physiological measurements across a population of neurons. Conclusions: A weighted normalization model, in which all parameters are derived from the statistics of an ensemble of natural images, can account for a variety of surround suppression effects, consistent with the hypothesis that visual neural computations are matched to the statistics of natural images.

Related pubs: nips-98 | Asilomar conference paper

I present a parametric statistical model for visual images in the wavelet transform domain. The model characterizes the joint densities of coefficients corresponding to basis functions at adjacent spatial locations, adjacent orientations, and adjacent spatial scales. The model is consistent with the statistics of a wide variety of images, including photographs of indoor and outdoor scenes, medical images, and synthetic (graphics) images, and has been used successfully in applications of compression, noise removal, and texture synthesis.

The model also suggests a nonlinear method of removing these dependencies, which I call ``normalized component analysis'', in which each wavelet coefficient is divided by a linear combination of coefficient magnitudes at adjacent locations, orientations and scales. This analysis provides a theoretical justification for recent divisive normalization models of striate visual cortex. Furthermore, the statistical measurements may be used to determine the weights that are used in computing the normalization signal. The resulting model makes specific predictions regarding non-specific suppression and adaptation behaviors of cortical neurons, and thus offer the opportunity to test directly (through physiological measurements) the ecological hypothesis that visual neural computations are optimally matched to the statistics of images.

Physiological recordings by Recanzone, Wurtz and Schwarz (1997), and other labs, indicate a decrease in the time-averaged response of directionally selective MT neurons to a stimulus moving in the preferred direction when that stimulus is paired with one moving in a non-preferred direction. Similarly, there is an increase in the response to an anti-preferred stimulus when it is paired with one moving in a non-preferred direction. In fact, the response to such complex stimuli is approximately the average of the responses to each of the moving components. We implemented a variant of the model by Simoncelli and Heeger (1998), in order to examine its responses to such stimuli. The model consists of two stages corresponding to visual areas V1 and MT, with each stage computing a weighted linear combination of inputs, followed by rectification and divisive normalization. The V1 stage contains directionally selective motion-energy neurons, and the MT stage selectively combines afferents of V1 neurons over a range of spatio-temporal orientations, to produce a velocity-selective response. In our model, the feedback normalization signal for each stage is computed by time-averaging and delaying the summed responses of all neurons in that stage. The model is able to replicate the averaging behavior described above, primarily as a result of the second stage of normalization. In addition, the time delay and low-pass filtering of the normalization signal produce transient temporal dynamics in the model which are qualitatively similar to those of MT responses.

More recent: Nature Neuroscience article.

Purpose: Several successful models of cortical visual processing are based on linear transformation followed by rectification and normalization (in which each neuron's output is divided by the pooled activity of other neurons). We show that this form of nonlinear decomposition is optimally matched to the statistics of natural images, in that it can produce neural responses that are nearly statistically independent. Methods: We examine the statistics of monochromatic natural images. One can always find a linear transformation (i.e., principal component analysis) that eliminates second-order dependencies (correlations). This transform is, however, not unique. Several authors (e.g., Bell & Sejnowski, Olshausen & Field) have used higher-order measurements to further constrain the choice of transform. The resulting basis functions are localized in spatial position, orientation and scale, and the associated coefficients are decorrelated and generally more independent than principal components. Results: We find that the coefficients of such transforms exhibit important higher-order statistical dependencies that cannot be eliminated with linear processing. Specifically, rectified coefficients corresponding to coefficients at neighboring spatial positions, orientations and scales are highly correlated, even when the underlying linear coefficients are decorrelated. The optimal method of removing these dependencies is to divide each coefficient by a weighted combination of its rectified neighbors. Conclusions: Our analysis provides a theoretical justification for divisive normalization models of cortical processing. Perhaps more importantly, the statistical measurements explicitly specify the weights that should be used in computing the normalization signal, and thus offer the opportunity to test directly (through physiological measurements) the ecological hypothesis that visual neural computations are optimally matched to the statistics of images.

I present a simple statistical model for images in the wavelet transform domain. The model characterizes the joint densities of coefficients at adjacent spatial locations, adjacent orientations, and adjacent spatial scales. The model accounts for the statistics of a wide variety of images. The model also suggests a nonlinear form of optimal representation, which I call ``normalized component analysis'', in which each wavelet coefficient is divided by a linear combination of coefficient magnitudes corresponding to basis functions at adjacent locations, orientations and scales. These statistical results provide theoretical motivation for the normalization models that have recently become popular in modeling the behavior of striate cortical neurons. In addition, I'll demonstrate the power of the decomposition for applications such as image compression, enhancement and synthesis.

More recent: Nature article.

Purpose: As an observer moves towards a surface, the visual image of the surface expands over time. Traditional approaches to measuring this expansion rely on computing the divergence of the local flow field. A complementary approach which would work well in contexts with poor flow information would be to measure shifts in the Fourier amplitude spectra of textures over time (analagous to size changes). To test whether the visual system uses the information provided by such a measure, we have created a set of novel stimuli which contain, on average, no local flow. We filtered successive frames of spatio-temporally white noise with band-pass spatial filters whose peak frequency varied in inverse proportion to time. The resulting stimulus is temporally uncorrelated, but contains changes in spatial fourier amplitude spectrum consistent with a constant expansion rate. We tested whether subjects could consistently match the expansion rate of such stimuli, which have no local flow information, to the expansion in random dot cinematograms designed to have no change in their Fourier amplitude spectrum over time. Methods: A temporal 2AFC task was employed to find points of subjectively equal expansion between the two types of stimuli. Several rates of expansion were tested and the start and end frequencies in the textured, non-flow stimuli were randomized between trials. Results: The matched expansion rates of the non-flow texture stimuli were monotonic and nearly linear with the true expansion rates of the dot (flow) stimuli. Settings were also consistent across different start and end frequencies. Conclusions: The results suggest that the visual system can use the change in the amplitude spectra of textures over time to make judgments about expansion.

More recent: Nature Neuroscience article.

Purpose: Local image translations have a simple characterization in the spatio-temporal frequency domain: the power spectral density of a translating pattern lies on a plane passing through the origin. The orientation of the plane specifies the velocity of the translation. To efficiently measure local velocities the visual system should selectively pool the outputs of the early spatio-temporal filters whose peak frequencies lie in a given plane. This kind of selective pooling creates velocity tuned mechanisms. We performed psychophysical experiments to test for such preferential pooling mechanisms. Methods: Using a 2-AFC discrimination paradigm, we measured signal power thresholds for detecting filtered noise signals embedded in temporally white noise. The signals were samples of spatio-temporal gaussian white noise filtered by one of two possible configurations of 11 band pass filters: planar or 'scrambled'. In the planar configuration, the 11 filters were arranged to form an annular ring centered on a specific plane in frequency space. In the scrambled configuration, the planar configuration of filters was modified by inverting the sign of the temporal frequency of 5 of the 11 filters. The two sets of signals thus constructed had equivalent temporal and spatial frequency fingerprints, considered independently, but differed in whether or not the signal power was concentrated around a single plane in frequency space. Experiments were run using two different noise patterns - noise which was both temporally and spatially white and noise which was temporally white but was spatially filtered to have the same spatial frequency fingerprint as the signal. The latter noise was used to eliminate the possibility of using a purely spatial cue for detection. Results: Detection thresholds were about 40% lower for the planar configurations of spatio-temporal signal power than for the scrambled configurations. This significant difference was enhanced to about 65% in the noise condition which eliminated the spatial structure cue. Conclusions: The results are consistent with the hypothesis that local translation detection is mediated by mechanisms which selectively pool planar configurations of power in the spatio-temporal frequency domain.

Model description: Vision Research article.

Purpose: To test and refine a velocity-representation model for pattern MT cells (Simoncelli & Heeger, ARVO 1994). The model consists of two stages, corresponding to cortical areas V1 and MT. Each stage computes a weighted linear sum of inputs, followed by halfwave rectification, squaring, and normalization. The linear stage of an MT cell combines outputs of V1 cells tuned for all orientations and a broad range of spatial and temporal frequencies. The resulting MT response is tuned for the velocity (both speed and direction) of moving patterns. Methods: We recorded the responses of MT neurons to computer-generated visual targets in paralyzed and anesthetized macaque monkeys using conventional techniques. Results: We measured direction-tuning curves for sinusoidal grating stimuli over a wide range of temporal frequencies. The model predicts that such curves should become bimodal at very low temporal frequencies, and this prediction is supported by the data. We measured temporal frequency tuning curves at a wide range of spatial frequencies and found that the shifts in peak tuning frequency are consistent with the model. Finally, we used a drifting sinusoidal grating additively combined with a random texture pattern moving at the neuron's preferred speed and direction to probe the shape of the hypothesized linear weighting function used to construct a model MT pattern cell from V1 afferents. Conclusions: The model is able to account for the data, which may in turn be used to better specify such details as the shape of the linear weighting function in the MT stage.

More recent: Vision Research article.

Purpose: The classic motion aftereffect is motion illusion induced by adaptation to a moving stimulus. Last year at ARVO, we reported that adaptation to translational motion stimuli induced a bias in the perceived direction of motion (DOM) of subsequent motion stimuli. We hypothesized that a similar bias would occur in perceived speed. We have performed experiments to measure the full velocity bias induced by motion adaptation. Methods: Stimuli were presented in two circular patches, on either side of a fixation point. The adaptation stimulus was presented for 10 second intervals, and consisted of a patch of constant-velocity random dots (CVRDs) and a patch of dynamic random noise. The subject then simultaneously viewed a test stimulus at the location of the adapting dots, and a match stimulus at the location of the noise. Both test and match consisted of CVRDs. The subjects performed a matching task, in which they reported whether the test and match velocities appeared the same or different. The collected could thus be used to determine the point of subjective equality. Results: Adaptation produces notable biases in the perceived speed of test stimuli. Specifically, test stimuli that are moving slower than the adaptation speed are matched by stimuli moving slower than the actual speed of the test stimuli. Similarly, test stimuli that are moving faster than the adaptation speed are matched by stimuli that are moving faster than the test speed. Conclusions: These results are consistent with a motion mechanism which explicitly represents speed. They also lend support to the hypothesis that the two-dimensional quantity of velocity (i.e., speed and DOM) is explicitly represented by the visual system.

Purpose: The coherence of moving square-wave plaids depends on a number of stimulus parameters: plaid angle (Q), grating speed (Sg), contrast (c), and period (p). Last year at ARVO, we explored the dependence on the plaid angle and the grating speed. We found that coherence depended on both of these parameters: this dependence is best understood via a reparameterization in terms of pattern speed (Sp = Sg / cos(Q)). When Sp is below a critical speed (roughly 5 deg/sec), the plaid is more likely to be seen as coherent. Above this critical speed, the plaid has the appearance of two gratings sliding transparently over each other. This year, we examined the effect of contrast and component period on the coherence of square-wave plaids. Methods: Subjects were presented with symmetric square-wave plaids of varying period and were asked whether the stimuli appeared transparent or coherent. In a second experiment, subjects judged the coherence of symmetric square-wave plaids of varying contrast. Results: The experiments reveal that both contrast and period affect the perceived coherence of the stimuli: gratings of higher contrast and gratings of smaller period appear more coherent. For fixed period and contrast, the effect of varying plaid angle and grating speed is consistent with our previous experiments: coherence is determined by the pattern speed relative to a critical speed. However, the current experiments reveal that this the critical speed depends on the stimulus contrast and period. Conclusions: These results suggest that the primary determinant of square-wave plaid coherence is the pattern speed. This behavior may be explained by a model for velocity perception with a built-in preference for slower speeds.

More recent: Vision Research article.

Purpose: We describe a model of MT cell responses that explains a variety of neurophysiological findings. Methods: The model (first presented in Simoncelli & Heeger, ARVO '93) consists of two stages, corresponding to cortical areas V1 and MT. Each stage computes a weighted linear sum of inputs, followed by halfwave rectification, squaring, and normalization (in which the output is divided by the pooled activity of a large number of cells). Model V1 cells are tuned for spatio-temporal frequency, and model MT cells are tuned for image velocity. The linear weighting function of a model V1 cell determines its orientation and direction selectivity. The weighting function for a particular V1 cell is only mildly constrained by the model, but the relationship between the cell weighting functions is heavily constrained. The linear weighting function of a model MT cell determines its velocity (both speed and direction) selectivity. Again, the individual weighting functions are only mildly constrained, but the relationship between cells is precisely specified. The free parameters of the model are the overall frequency response of the V1 stage, the overall velocity response of the MT stage, the semi-saturation constants used in the two normalization operations, and the spontaneous firing rates in the two stages. Results: We demonstrate that the model is consistent with a wide range of experimental data. In particular, we show that the model explains data published by Maunsell & Van Essen (1983), Albright (1984), Movshon et. al. (1985), Allman (1985), Rodman & Albright (1989), Orban (1993), Britten et al (1993), and Snowden et al (1993). Conclusions: Our simulation results provide compelling evidence that this model accounts for much of the published data recorded from MT cells. This theoretical work also leads to several testable predictions that will be discussed.

Purpose: We performed psychophysical experiments to determine the rules governing the perception of transparency in additive square-wave plaids. Methods: Subjects were presented with a randomized sequence of square-wave plaids of varying grating speed, grating orientation and plaid intersection luminance. The two gratings were symmetrically oriented about vertical, with fixed and equal period and duty-cycle. Presentations lasted two seconds, with a three second inter-trial interval. Subjects were asked whether the stimulus appeared to be transparent or coherent. Results: Our experimental results suggest that the perception of transparency is primarily governed by 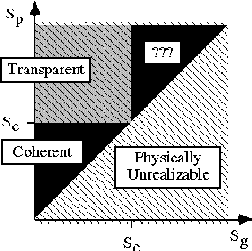the pattern speed and the grating speed. In particular, when the pattern speed exceeds a certain critical speed (Sc), the plaid is more likely to be seen as transparent. Furthermore, when the grating speed exceeds the critical speed, subjects report being unable to make clear judgments. This result is illustrated in the idealized diagram of subject response versus pattern speed (Sp) and grating speed (Sg) shown to the right. Further studies suggest that varying the luminance of the plaid intersections (see Stoner, et. al., 1990) seems to affect the percept of transparency only when the pattern speed is close to the critical speed. Conclusions: The existence of such a critical speed suggests that the human visual system may have a perceptual preference for slower speeds. This data and the original data of Stoner, et. al. is consistent with a fairly simple energy-based model for velocity computation in which the representation of velocity is speed-limited.

More recent: Vision Research article.

Purpose: The perceived direction of motion (DOM) of a drifting sinusoidal grating can be altered by first adapting to a grating or plaid drifting in a different direction (Lew, et. al., ARVO, 1991). We have designed experiments using similar motion-adaptation effects to demonstrate that the visual system represents motion information with a population of mechanisms that are tuned for velocity (i.e., both speed and direction). Methods: Subjects viewed an adapting stimulus followed by a drifting sinusoidal test grating, and were asked to report (by positioning a directional arrow with a mouse) the perceived DOM of the test. Test gratings were of variable spatial and temporal frequency, and the adapting stimulus was either a drifting grating, plaid, or correlated random dots. Results: We found that the effect on the perceived DOM of the test was always of the same form, regardless of the type of adapting stimulus. In particular, for test gratings with DOMs less than $90^{\circ}$ from that of the adapting stimulus,\footnote{\small Adapting DOM is defined as the normal direction for gratings, and the pattern (or intersection-of-constraints) direction for plaids.} the DOM was strongly biased away from the adapting DOM. For gratings with orientations more than $90^{\circ}$ from the adapting DOM, the DOM was biased slightly toward the adapting DOM. For grating adaptation, shifts of the test spatial frequency of up to an octave from that of the adapting grating modestly reduce the magnitude of the effect. Conclusions: Since these effects are not strongly dependent on the type of adapting stimulus (i.e., grating, plaid or correlated dot pattern), or the spatial frequency (in the case of grating adaptation), we argue that they cannot be simply explained by adaptation of spatio-temporal energy mechanisms. They are, however, consistent with a mechanism that explicitly represents velocities.

More recent: Vision Research article.

We have constructed a general model for computing image velocities that is capable of representing multiple velocities occurring at occlusion boundaries and in transparently combined imagery. The behavior of the model is illustrated in the figure below. On the left are two transparently overlaid fields of random dots, moving in different directions. On the right is the output of the model, a bimodal distribution over velocity. The brightness at each point is proportional to the response of a velocity-tuned mechanism.

The computation is performed in two stages. The first stage computes normalized spatio-temporal energies, analogous to complex cells. The second stage uses the same operations (linear combination followed by normalization) to construct a velocity-tuned response, analogous to a hypothetical velocity cell as has been postulated to exist in area MT. We demonstrate the behavior of the model on a set of stimuli, indicating its consistency with human motion transparency phenomenology.

How are transparently combined moving images correctly interpreted as a set of overlapping objects? To address this question, we advocate a framework consisting of a local motion mechanism which can operate in the presence of transparency, as well as a global pooling mechanism that integrates information across space.

Previously (ARVO-92), we outlined a model of transparent motion perception that used layers to represent multiple motions. Locally, the model tested for the presence of a particular velocity despite the presence of other velocities at the same location. This was accomplished by applying first-order "nulling" filters to remove the energy due to a possible conflicting velocity, and then testing for the chosen velocity.

Here we present a new method for testing the presence of a local velocity in an image, using "donut" mechanisms formed from the weighted combination of spatio-temporal energy units. This method has the advantage over nulling filters that it does not require the application of multiple prefilters for each tested velocity, can potentially handle regions with 3 motions, and seems to be more biologically plausible.

Our global layer selection mechanism attempts to account for the local velocity distributions with a small set of global basis functions (translations, expansions, rotations). Using donut mechanisms permits a simplified layer selection optimization, in which inhibition between basis functions is determined by the product of their weight coefficients. With this scheme, we demonstrate the decomposition of image sequences containing additively combined multiple moving objects into a set of layers corresponding to each object.

More recent: Nature Neuroscience article.

The perceived velocity of a moving pattern depends on its spatial structure. A number of researchers have used sine-grating plaid patterns to study this dependence. We describe a model for the computation and representation of velocity information in the human visual system that accounts for a variety of these psychophysical observations. In contrast with previous models, our model does not explicitly compute or rely on the normal velocities of the component gratings. It takes image intensities as input, and produces a distributed representation of optical flow as output, without invoking special-case computations or multiple pathways.

The model is derived as a Bayesian estimator, as in our ARVO-90 presentation, and is implemented in two stages. The first stage computes normalized spatio-temporal energy. The normalization, specified by the Bayesian estimator, is a form of automatic gain control in which each energy output is divided by an appropriate sum of energies plus a small offset (i.e., a semi-saturation constant). The second stage of the model computes a distributed representation of velocity via a linear summation of the STE outputs. The velocity estimate is given by the peak (or mean) location in the distribution. In accordance with the Bayesian approach the model incorporates a prior bias toward slower speeds, implemented by adding a small offset to two of the motion energies. Thus, the model has two parameters: the semi-saturation constant for the gain control, and the prior bias.

We show that this model is consistent with many recent psychophysical experiments on the perception of sine grating plaid velocities, including observed deviations from the intersection-of-constraints solution. For appropriate values of the two parameters, the model accounts for: 1) the data of Stone et. al. describing the effects of contrast on plaid direction; and 2) the data of Ferrera and Wilson describing the perceived speed and direction of plaids.

The human visual system can easily distinguish multiple motions that are transparently combined in an image sequence. A model for the perception of transparent motion must address two questions: 1) what local motion measurements are made? and 2) how are these local estimates used to group coherently moving regions of the scene?

Two current computational approaches provide interesting insights into these issues. The algorithm of Shizawa and Mase directly computes two velocity vectors for each location in the image, but does not address the problem of perceptual grouping of coherently moving regions of the scene. The algorithm of Bergen et. al. computes two global affine optical flow fields, but does not explicitly determine which portions of the scene correspond to each of these velocity fields. Furthermore, the local measurements used are only capable of determining a single velocity estimate at each point, and will thus have difficulty with pure transparency.

We have extended our previous model for layered image segmentation (ARVO-91) by incorporating the advantages of these two approaches. The previous model performs a decomposition of an image sequence into non-overlapping regions of support (``layers'') corresponding to coherent single motions in the scene. This is accomplished by testing many motion hypotheses, and enforcing mutual inhibition between hypotheses that are supported by the same image data. The new model computes direct estimates of transparent motions, using the local velocity measurements proposed by Shizawa and Mase. Each layer performs grouping based on a model of additively combined image regions, each undergoing global affine motions. The multi-layer competition scheme proceeds as before, producing a set of (possibly overlapping) layers that parsimoniously describes the visual scene. We demonstrate the use of this model on transparently moving imagery.

More details in PhD Thesis.

We will compare three different approaches to low-level motion analysis: 1) gradient techniques based on spatial and temporal derivatives (e.g., Horn and Schunk); 2) spatio-temporal energy methods, based on tuned filters (e.g., Adelson and Bergen); and 3) regression methods, which find a best-fitting plane in spatio-temporal frequency (e.g., Heeger). Each of these has, at some point, been proposed as a model for low-level motion processing in human vision. We will demonstrate that these approaches, although based on different assumptions, are very closely related. In fact, when they are formulated as velocity estimators, and when the parameters of each model are suitably chosen, the three methods are computationally equivalent. Thus, it is difficult to experimentally determine their relative validity as models of human visual processing. Furthermore, in their equivalent form, all three techniques extract only a single motion vector for each spatial position in the visual field, and so they are incapable of representing the multiple motions that occur near occlusion boundaries and in situations of transparent motion. We suggest extensions of these approaches which can handle these cases.

More info: Book chapter on QMF pyramids; Journal article on steerable pyramid.

Images contain information at multiple scales, and pyramids are data structures that represent multi-scale information in a natural way. We discuss a number of types of pyramids that we have applied to a number of applications in image coding and image analysis. The Gaussian and Laplacian pyramids are useful as a front-end representation for many tasks in early vision, and the Laplacian pyramid is reasonably efficient for image coding. Better image data compression can be achieved by using pyramids based on quadrature mirror filters (QMF's), which are closely related to a class of wavelet transforms. QMF pyramids offer a representation that is localized in space and spatial frequency, is self-similar, and is orthogonal. Separable QMF pyramids are quite useful for image coding, but they involve some difficulties with mixed orientations. A QMF pyramid based on a hexagonal sampling lattice exhibits good orientation tuning properties, and is likely to be more useful for general vision applications including models of early vision. We have also explored pyramids based on steerable filters; these pyramids are overcomplete and are less efficient than the QMF pyramids, but offer excellent properties for orientation analysis, image enhancement, and several other tasks. By understanding the strengths and limitations of these representations, we hope to gain insights into the problems confronting both artificial and biological visual systems.

The extraction of 3D motion from images is a difficult but important task for natural and artificial vision systems. Methods for recovering 3D motion from images typically compute optical flow fields from sequences of images, and then combine this information to obtain global estimates of rigid-body motion. These techniques often fail in the presence of noise or the aperture problem, and cannot be cast as physiologically plausible models.

We recast the problem in the framework of estimation theory, using probability distributions to describe successive intermediate representations of motion information. Previously, researchers have described a mapping from images to distribution of motion energy (analogous to the outputs of direction selective cortical cells), and then to distributed representations of of image velocity (analogous to the outputs of MT cells). We discuss an extension of the Heeger/Jepson algorithms that computes a distributed representation of image velocity, thus avoiding the biological implausibility of explicit velocity representations. Uncertainties and ambiguities due to noise or the aperture problem may be directly included in the distributions of motion energy, and propagated through the computation to alter the final distribution of the 3D motion parameters. We also discuss extensions to handle situations involving motion transparency, motion occlusion boundaries, and independently moving objects.

An image representation is efficiently sampled if the number of coefficients equals the number of degrees of freedom in the represented image. Orthogonal transforms (e.g. the Fourier transform), and some non-orthogonal transforms (e.g. the Gabor transform) are efficiently sampled. Some pyramid representations, such as Burt and Adelson's Laplacian pyramid and Watson's cortex transform, are not efficiently sampled, being oversampled by a factor of 4/3. Recently, efficiently sampled pyramids based on quadrature mirror filters have been developed; they capture a number of useful properties that are similar to those found in the human visual system, such as tuning in SF and orientations, and localization in space. These QMF pyramids perform quite well at image data compression. However, they have some problems with shift-variance that may limit their performance in computational vision and modeling. We argue that a modest amount of oversampling can offer significant advantages in both human and machine vision.