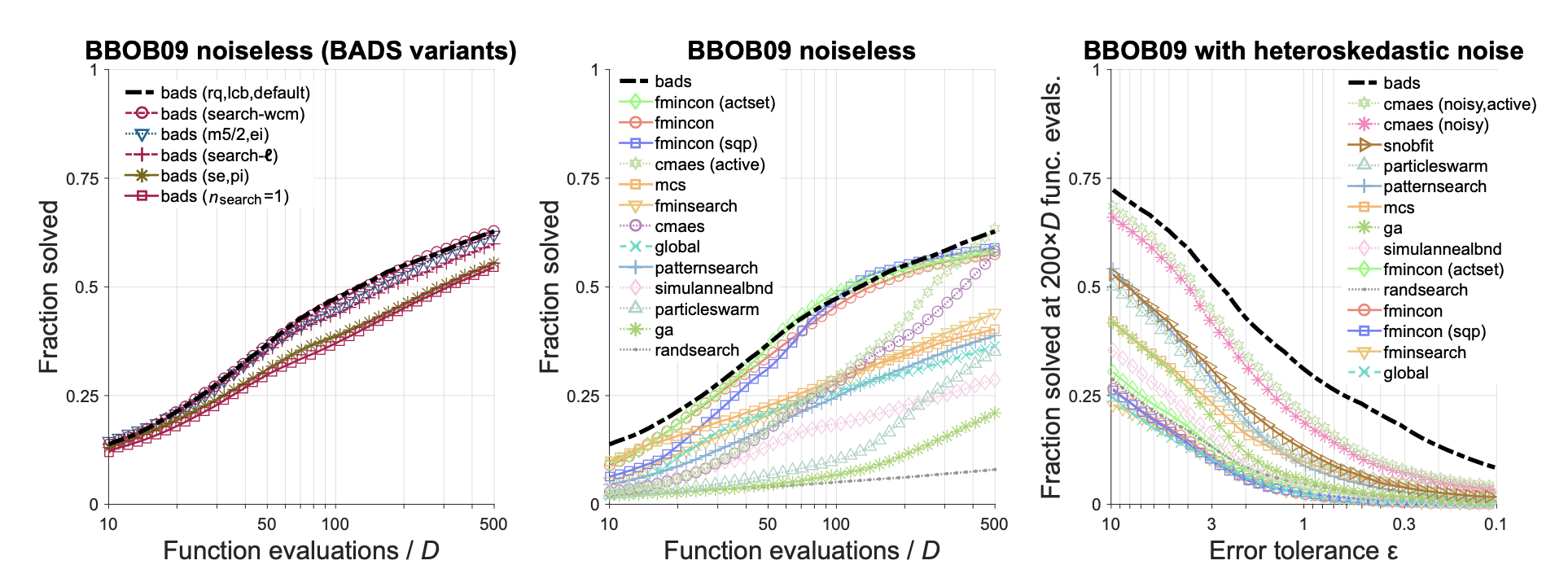
Bayesian Adaptive Direct Search (BADS)
Source paper: Acerbi, L., & Ma, W. J. (2017). Practical Bayesian optimization for model fitting with Bayesian Adaptive Direct Search. Advances in neural information processing systems, 30.
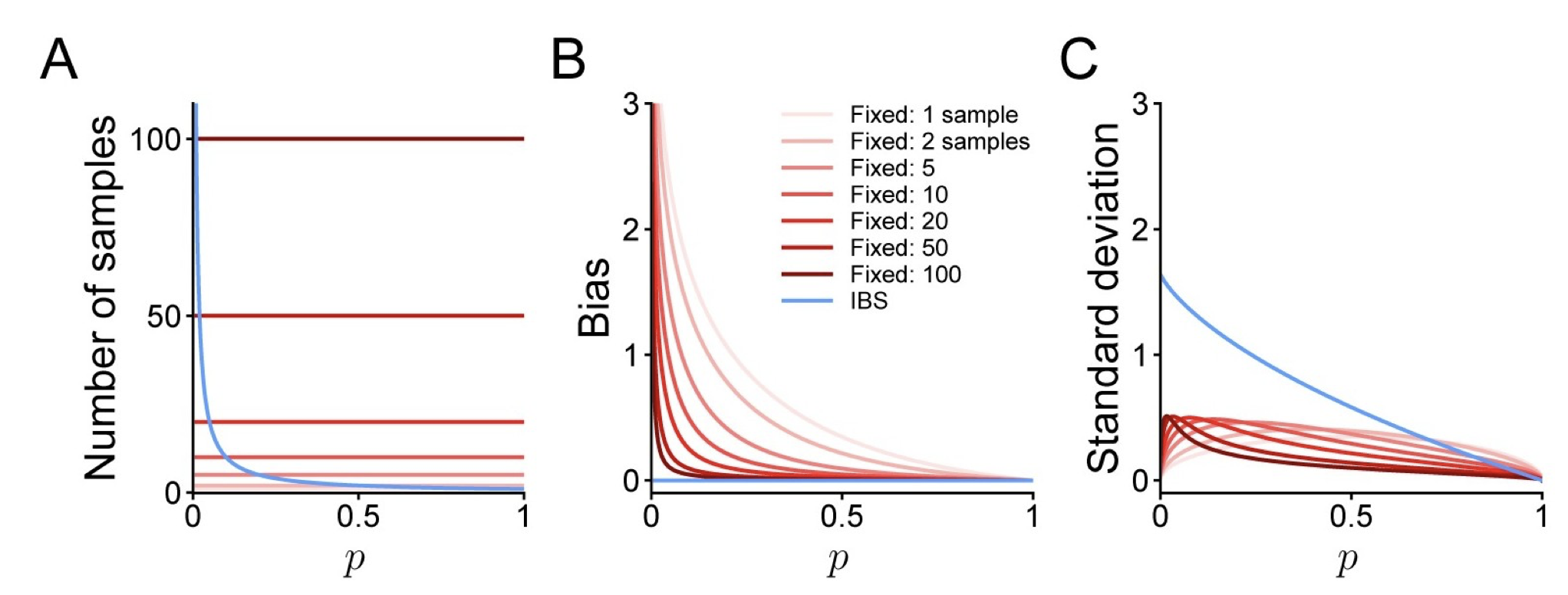
Inverse Binomial Sampling (IBS)
Source paper: van Opheusden, B., Acerbi, L., & Ma, W. J. (2020). Unbiased and efficient log-likelihood estimation with inverse binomial sampling. PLoS computational biology, 16(12), e1008483.
Tutorial in Bayesian statistics
Prerequisites: basic probability theory, basic frequentist statistics
-------------------------------------------------------------------------------------------
Presenter: Gianni Galbiati
Video | Slides | Slides (with notes)
Code example (presidential heights) | Code example (Aspen’s change detection task)
Prerequisites: basic probability theory, basic frequentist statistics
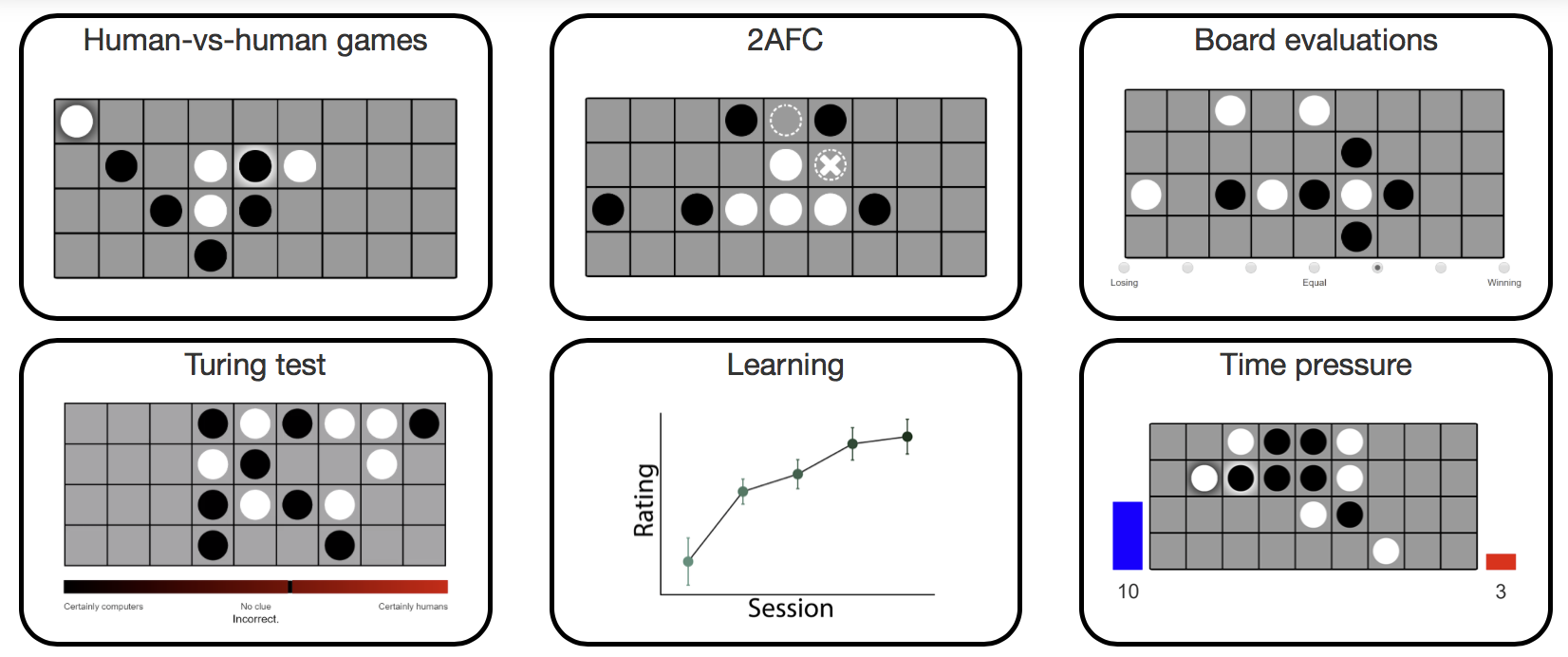
Four-in-a-row
In the paper Revealing the impact of expertise on human planning with a two-player board game (2021), we conducted a set of experiments on the game four-in-a-row, played on a 4-by-9 board. We also introduced a computational model of human moves. Here, you can try out the experiments and explore the data.
Code | Try experiment | Explore dataSource paper: van Opheusden, B., Galbiati, G., Kuperwajs, I., Bnaya, Z., & Ma, W. J. (2021). Revealing the impact of expertise on human planning with a two-player board game.
Variable-precision (VP) models
The variable-precision model is currently (2016) the best available model of set size effects in visual working memory. In this model, the observer has a noisy representation of all items in a memory array. The precision of this representation is itself modeled as a random variable - possibly reflecting fluctuations in attention. Mean precision decreases monotonically with set size. The VP model consistently outperforms the fixed-capacity, item-limit model by Pashler 1988 and Cowan 2001, and more recent variants. Here, we provide simple, stand-alone Matlab scripts to analyze data from two common paradigms: delayed estimation and change detection. In its basic form, the model has three parameters (for change detection) and four (for delayed estimation). Note that the VP model here (with a gamma distribution on precision) is slightly different from the one implemented in MemToolbox. Email us if you have any questions.
Source papers:1. Van den Berg, R., Shin, H., Chou, W. C., George, R., & Ma, W. J. (2012). Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences, 109(22), 8780-8785.
2. Keshvari, S., Van den Berg, R., & Ma, W. J. (2012). Probabilistic computation in human perception under variability in encoding precision. PLoS One, 7(6), e40216.
3. Keshvari, S., Van den Berg, R., & Ma, W. J. (2013). No evidence for an item limit in change detection. PLoS computational biology, 9(2), e1002927.
Light (9.2 MB) - large .mat files containing analysis output left out; however, they can be generated using the provided code
Delayed-estimation benchmark data and factorial model comparison
Delayed estimation is a psychophysical paradigm developed in 2004 by Patrick Wilken and Wei Ji Ma, that is used to probe the contents of working memory. Observers remember one or multiple items and after a delay, report on a continuous scale the feature value of a stimulus at one probed location. This benchmark data set contains data from 10 experiments and 6 laboratories. Additional data sets are welcome. Email us if you have any to add. Below, we also provide complete code to analyze the data.
Source papers:1. Wilken, P., & Ma, W. J. (2004). A detection theory account of change detection. Journal of vision, 4(12), 11-11.
2. Zhang, W., & Luck, S. J. (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453(7192), 233-235. | Zhang lab | Luck lab
3. Bays, P. M., Catalao, R. F., & Husain, M. (2009). The precision of visual working memory is set by allocation of a shared resource. Journal of vision, 9(10), 7-7. | Bays lab | Husain lab
4. Rademaker, R. L., Tredway, C. H., & Tong, F. (2012). Introspective judgments predict the precision and likelihood of successful maintenance of visual working memory. Journal of vision, 12(13), 21-21. | Tong lab
5. Van den Berg, R., Shin, H., Chou, W. C., George, R., & Ma, W. J. (2012). Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences, 109(22), 8780-8785.
6. Van den Berg, R., Awh, E., & Ma, W. J. (2014). Factorial comparison of working memory models. Psychological review, 121(1), 124.
Change detection
Change detection is a classic paradigm developed by W.A. Phillips (1974) and Harold Pashler (1988), to assess the limitations of visual short-term memory. Our lab has made two improvements to this paradigm: first, we vary the magnitude of change on a continuum, so that we can plot entire psychometric curves and thus have more power to compare models. Second, we test new models, especially noise-based (continuous-resource) models, and found that they do better than item-limit (slot) models.
References on the concepts:Light (9.2 MB) - large .mat files containing analysis output left out; however, they can be generated using the provided code