When we first discussed linear systems theory, it was in the context of audition
where we describe an auditory signal as a single value, pressure, as a function
of a single variable, time. Linear systems theory has also been applied extensively
to vision, but there the stimulus is substantially more complicated. At a minimum,
you talk about an image (i.e., a picture,
a retinal image, a neural image) which is a function of the two spatial dimensions
x and y. But, if you are interested in temporal
sensitivity as well (e.g., to understand visual motion), then you have a signal
that is a function of three variables: x, y, and t (i.e., a movie, or sequence of images).
In audition, the basic stimulus used in linear systems theory is the sine wave.
The analogous stimulus for vision is the sine wave grating. Such gratings can vary
in spatial frequency (measured in cycles/degree, for a retinal image), orientation,
phase and contrast.

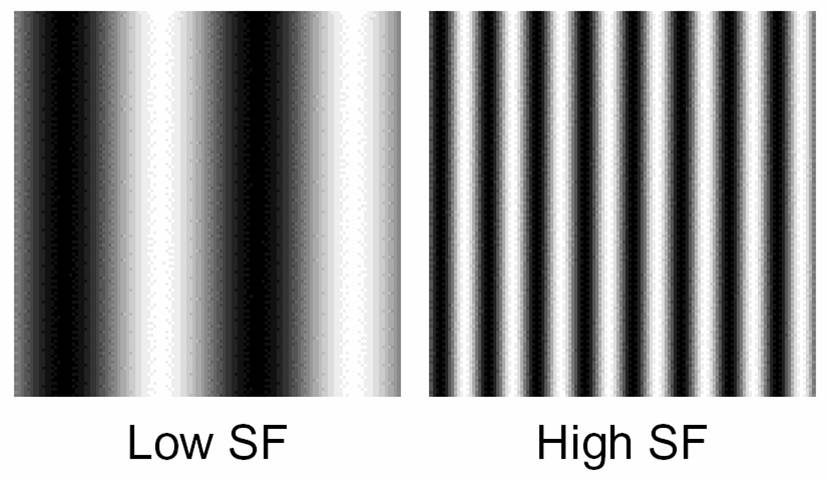
Low and high spatial frequency sine wave gratings
Contrast for sine wave gratings is usually defined as Michelson contrast for which the formula is
(Imax-Imin)/(Imax+Imin) or (Imax-Imin)/(2 Imean). This is a number that ranges
from zero (the bright and dark bars have the same intensity as the mid-gray,
in other words the grating is invisible) to one (the bright bars are twice the
intensity of the mean and the dark bars are black). Note that this definition
is the same as the definition we've used previously, Weber
contrast or ΔI /
I, where ΔI means the increment of the bright
bar above the mean (Imax-Imean)
and I stand for the mean intensity
(I=Imean).



The characterization of a system in linear systems theory is the Modulation
Transfer Function (MTF), i.e., the degree to which different frequencies
are amplified or attenuated by the system. The behavioral analogy to the
MTF is the contrast sensitivity function
(CSF) which describes how sensitive an observer is to sine wave gratings
as a function of their spatial frequency. This is measured using a contrast
detection experiment wherein one determines the minimum contrast required
to detect sine wave gratings of various spatial frequencies. As usual, sensitivity
is defined as 1/(threshold contrast) (so if threshold is low, sensitivity
is high).

The figure above shows a pattern that increases in spatial frequency
from left to right (the bars get narrower), and decreases in contrast
from bottom to top (the bars get fainter). By tracing out the boundary
between visible and invisible you can make out the curved shape of your
CSF. The typical results of such a measurement follow:

The typical CSF is bandpass in nature. That is, you are most sensitive
for an intermediate range of spatial frequencies (around 4-6 cycles/degree),
and less sensitive to spatial frequencies both lower and higher
than this, much like the audiogram. The highest spatial frequency
you can see (the high frequency cutoff) determines your spatial
acuity, i.e., the finest spatial patterns you can see. This acuity
limit typically worsens with age.
The CSF is typically not thought of as the MTF of a single kind of neuron,
but rather an envelope of sensitivity over several underlying mechanisms,
each corresponding to neurons with differing preferred spatial frequencies
(i.e., with different sizes of receptive field; larger = lower spatial
frequency preference). A graph illustrating this follows:

In the figure above, four spatial frequency channels are illustrated, and the
notion is that the CSF represents the sensitivity pooled over those
underlying channels, i.e., sensitivity is primarily determined by
whatever channel (or set of neurons) is most sensitive to the stimulus.
Now, what does this parsing of the stimulus into different frequency
bands do for the observer?

As you can see, the low frequency filters provide information about large objects,
shadows, and other smooth, gradual changes in intensity across the image.
The higher spatial frequency filters emphasize progressively finer details.
What evidence is there for the existence of multiple spatial frequency channels?
Well, first of all, there is the physiological evidence. In V1 and beyond,
for each location in the visual field there are neurons varying in preferred
spatial frequency, orientation, direction of motion, and so on. But, there
is behavioral evidence as well. First, consider the effects of adapting
to a particular spatial frequency. One begins by measuring the CSF as illustrated
in a figure above. Then, you have the observer stare at a particular sine
wave grating (e.g., 8 cycles/degree) for an extended period of time.
The visual system adapts to that
pattern, and any neurons or mechanisms that were sensitive to that pattern
become desensitized temporarily. If one re-measures the CSF while in that
adapted state, the results are as follows:
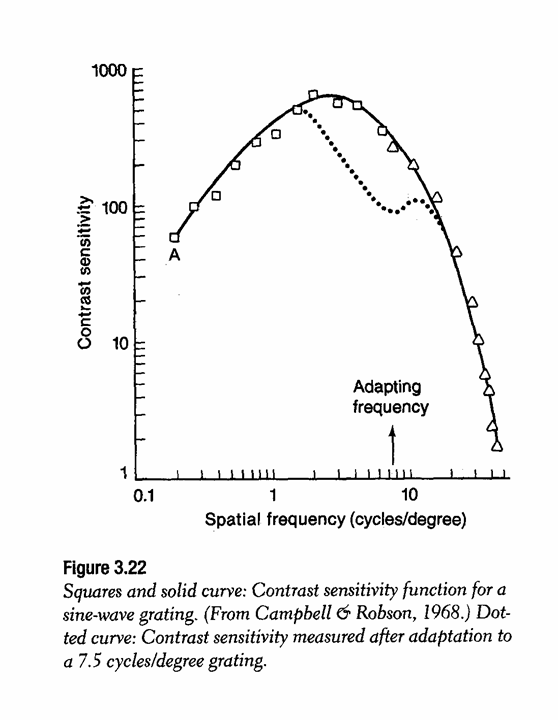
The dotted curve represents the post-adaptation CSF and, as you can see, sensitivity
is reduced, but only for gratings with spatial frequencies near that of
the adapting grating. The idea is that the spatial frequency channels sensitive
to the adapting grating now have reduced sensitivity due to all that stimulation,
but those with spatial frequency preferences distant from the adapter remain
unaffected. Spatial frequency adaptation not only affects threshold, but
also affects the appearance of supra-threshold gratings. After adaptation
to 10 cycles/degree (i.e., even narrower bars), an 8 cycle/degree
grating will appear to have an even lower spatial frequency (even wider
bars). Likewise, after adapting to 6 cycles/degree (i.e., wider bars) an
8 cycle/degree grating will appear to have an even higher spatial frequency
(even narrower bars). The explanation is illustrated here:
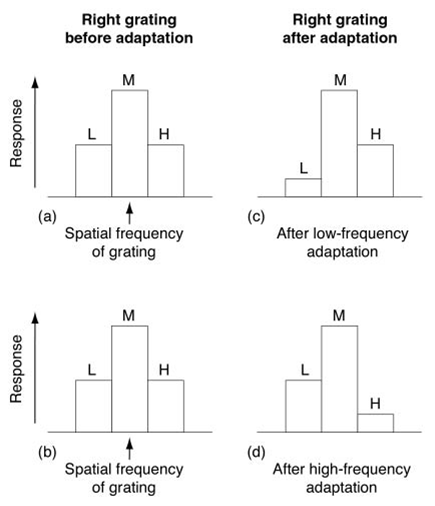
The idea is that adaptation to the higher spatial frequency desensitizes
the higher spatial frequency channels (those that "see" the higher frequency
grating). Then, when you display the 8 cycle/degree grating, the center
of the response profile shifts to lower frequencies (bottom-right graph
above). When you adapt to a lower spatial frequency grating, you see the
opposite shift in the response (upper-right graph). Similar shifts happen
with orientation and direction of motion, indicating that there are channels
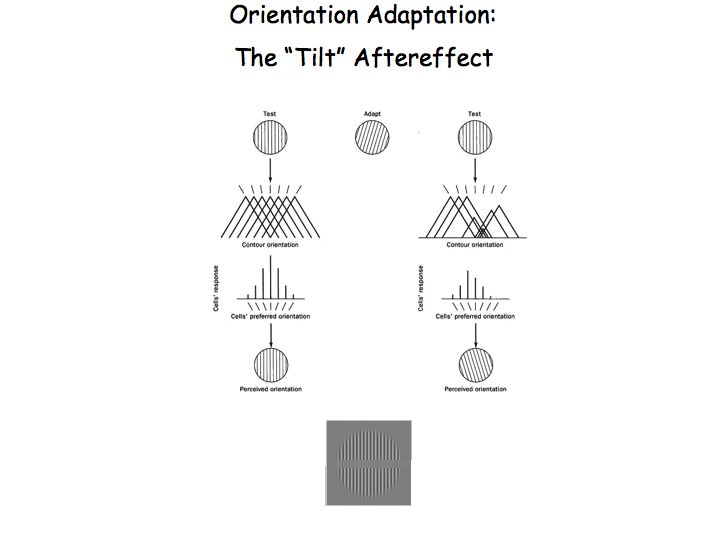
tuned for various orientaitions and directions of motion. For example, here's
an analogous explanation of the tilt after-effect based on orientation-tuned
channels. In this effect, one stares at, for example, a grating tilted slightly
top-to-the-right. After adapting, a vertical grating appears tilted slightly
top-to-the left because channels preferring leftward tilt are now responding
more strongly than those tuned to rightward tilt (because the latter were
more strongly adapted).
There are two other common methods of demonstrating the existence of multiple
spatial frequency channels psychophysically. The first is called summation.
There, the idea is that if you ask an observer to detect a combination of
two grating (literally added together on the screen), the sensitivity is
much higher if the two gratings are close in spatial frequency (so that
they are detected by the same channel) than when they are far different
in spatial frequency (so that they are detected by separate channels). A
third psychophysical paradigm is called masking. In this type of experiment, the observer
is asked to detect one test grating (with frequency f1) in the presence of another masking grating (with frequency f2). The masking grating is always present,
and the question is to what degree does it mask the test grating, making it harder to
detect. It turns out that the results lead to the same model. When the masking
grating is similar in spatial frequency to the test grating, masking is
strong, and when it is dissimilar, masking is weak. In other words, one
grating masks another only to the extent that both are detected by the same
channel.