Contents
%Lab 3: Functions, SVD, error correction, Vectorization, Saving and Loading
1 Functions
%Functions made: Width and deg2rad %Exercise 1: Make a rad2deg function %Exercise 2: Package the inner product logic we wrote last time into a %function %Exercise 3: Package the matrix multiplication logic from lab 2 into a %function
2 SVD! The most useful thing (for us) in Linear Algebra
%a) Verify the 3 things I so boldly asserted last week. %Remember: We did not derive or prove this. So let's at least check them for ii = 1:1%e5 %Let's try 100,000 times. To see if the SVD always works M = randn(2,2) %Create some random matrix M. Any matrix will do. This will represent the operations x = randn(2,2) %Create some random matrix x that represents data. [U,S,V] = svd(M) %Do the SVD on matrix M. C = M*x %To find out what the operations matrix does to the data, apply it %Check whether SVD of M and M do correspond to the same thing? D = U * S * V' * x %The other radical claim was that the SVD corresponds to a sum of outer %products. Let's convince ourselves that this is actually true. What if I %forgot a sign somewhere? SOP = (S(1,1).*(U(:,1)*V(:,1)')*x) + ... (S(2,2).*(U(:,2)*V(:,2)')*x) %We convinced ourselves by visual inspection that the SVD and M indeed %produce the same output. Generally speaking, that is not good enough - we %want to do this programmatically. C == D; %The problem with this is that MATLAB has enough numerical precision %to get you in trouble. It's not infinite, so it's not perfect, but there %are slight rounding errors somewhere in the 16th after-digit place %So we need to set the numerical precision we want %Setting numerical precision: C = round(C.*1000)./1000; %Setting numerical precision to 3 after comma digits %This works by multiplying by thousand, rounding, then dividing by 1000 %again. This might make a good function. Because you will want to %set the precision arbitrarily, user-defined. And you will use this a lot. %And it is clunky. D = round(D.*1000)/1000; C == D; %This is nice, but still requires visual inspection. %How do we reduce this output to a single number that tells %me whether it matches or not? %Idea: Let's sum them up and compare to the number of elements in the %matrix E(ii) = sum(sum(C == D)) == numel(C); %This presumes that C and D are %the same dimensionality, because we only check C. end %Exercise for the reader: %Do this with matrices of different dimensionalities %Convince yourself programmatically that SOP also corresponds to the others %I did this just for one case %Write a numerical precision function
M =
-1.5176 0.50836
-2.1421 0.39312
x =
0.3078 -1.3729
1.3686 0.67888
U =
-0.59101 -0.80667
-0.80667 0.59101
S =
2.6966 0
0 0.18259
V =
0.97342 -0.22902
-0.22902 -0.97342
C =
0.22863 2.4286
-0.12132 3.2078
D =
0.22863 2.4286
-0.12132 3.2078
SOP =
0.22863 2.4286
-0.12132 3.2078
3 Let's get a visual intuition for the SVD
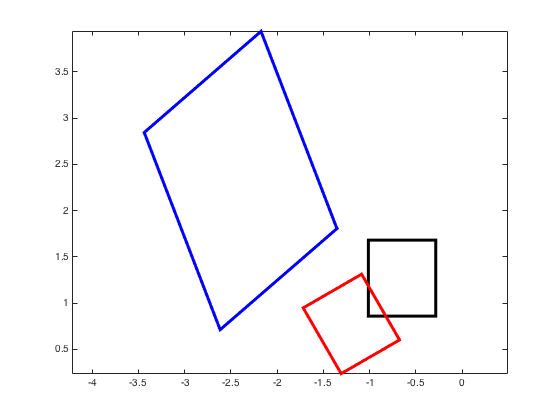
figure %Open a figure %Every rectangle (and we will illustrate everything here with a rectangle %can be defined by 4 numbers. The 4 numbers we will draw randomly %here are x-position and y-position of corner, width and height M = randn(1,4) %CornerX, CornerY, Width, Height %Now, we need to translate that into an x- and y-trace and plot those xTrace = [M(1,1), M(1,1)+M(1,3), M(1,1)+M(1,3), M(1,1), M(1,1)] yTrace = [M(1,2), M(1,2), M(1,2) + M(1,4), M(1,2) + M(1,4), M(1,2)] plot(xTrace,yTrace,'color','k','linewidth',3) axis equal shg %After generating the original rectangle, we now rotate it %Rotation is done by us through multiplication with orthogonal matrices %Later, we'll use one coming out of the SVD %Here, we'll use a designed one, so we can pick how much to rotate theta = degToRad(-30); %30 degrees in radians U = [cos(theta) sin(theta); -sin(theta) cos(theta)]; %Rotation matrix %Put the traces into a matrix so we can apply the rotation at once R(1,:) = xTrace; R(2,:) = yTrace; RR = U*R; %Matrix multiplication hold on %I want to see it in terms of the old coordinate system pause plot(RR(1,:),RR(2,:),'color','r','linewidth',3) S = [2 0; 0 3] %This will compress the first dimension by half and double the 2nd one SRR = S*RR; %Applying a stretch to the rotated rectangle. pause plot(SRR(1,:),SRR(2,:),'color','b','linewidth',3) %Exercise: Create a function where the user can input rotation angle, %stretch factors (one for each dimension) and an arbitrary matrix and it %outputs plots of the original matrix (rectangle) and the transformed one %Add the 2nd rotation. We only did one.
M =
-0.28529 0.85964 -0.72878 0.82052
xTrace =
-0.28529 -1.0141 -1.0141 -0.28529 -0.28529
yTrace =
0.85964 0.85964 1.6802 1.6802 0.85964
S =
2 0
0 3
4 Saving and loading
whos %Gives a list of variables in the workspace save('MyFirstVariables') %This saves all variables. If you want to save only some, you need to list them by name clear all %Delete everything in the workspace to show that the loading worked whos load('MyFirstVariables') %Load these variables again %If these files are *not* in your working directory (or path), you need to %give a path. Generally, we recommend to be in the path you need to be. %You can do this programmatically with cd - change directory
Name Size Bytes Class Attributes A 1000000x1 8000000 double B 999996x1 7999968 double C 2x2 32 double D 2x2 32 double E 1x1 1 logical M 1x4 32 double R 2x5 80 double RR 2x5 80 double S 2x2 32 double SOP 2x2 32 double SRR 2x5 80 double U 2x2 32 double V 2x2 32 double ans 2x2 4 logical cumsum 1x1 8 double ii 1x1 8 double n 1x50 400 double temp 500499x1 4003992 double temp1 1x50 400 double temp2 1x50 400 double theta 1x1 8 double timeWithCommand 1x1 8 double timeWithFind 1x1 8 double timeWithFunction 1x1 8 double timeWithFunctions 1x1 8 double timeWithLoop 1x1 8 double timeWithVector 1x1 8 double x 2x2 32 double xTrace 1x5 40 double yTrace 1x5 40 double
5 Error checking and error correcting code
%This is a little bit of an advanced topic, but we'll do just enough of it %for you to do the homework A = randn(2,3) B = randn(2,3) %C = A*B %Where they touch, they need to match. Here, they don't, so MATLAB throws an error %If MATLAB throws an error, execution of code is terminated. This can be %problematic. It makes sense to write code in a flexible fashion. Basically %anticipate that the user will do something ill-conceived and plan %accordingly. %MATLAB does this with try - catch statements try %This is blue. This is recognized by MATLAB as a program flow command. It modifies the program flow C = A*B %Do the best you can to do it. Of course we know it will fail catch %If you encounter an error in the course of programmatic affairs. By trying that. %Do this *instead* or *try this* instead %First thing: Tell the user that there was a problem disp('Error! You''re matrix dimensions did not match. That''s ok - we fixed that for you') C = A*B' %Transpose end
A =
-0.19824 -0.66304 -0.1039
-1.1714 1.6994 0.073608
B =
1.958 0.12326 0.81588
-0.68751 -0.34372 0.19284
Error! You're matrix dimensions did not match. That's ok - we fixed that for you
C =
-0.55463 0.34415
-2.0241 0.23543
6 Vectorization
%MATLAB is optimized to handle matrices - as it is an interpreted %language, loops will be slow. So, they should be avoided wherever %possible. It is almost always possible. So why ever use loops? They do %have their place - they always work and they are easy to understand. %a) Creating a vector with a million elements %First with a loop clear A tic %Starts the clock for ii = 1:1e6 A(ii,1) = ii; %Fill A from 1 to a million, via loop. Every time we go through it, we add a number end timeWithLoop = toc %Stops the stopwatch, and I want to save that number %With a function clear A tic A = linspace(1,1e6,1e6); timeWithFunction = toc %With a vector clear A %Clear because I don't want to confer an unfair advantage to the vector tic %Every time you call tick, a stopwatch is started A = 1:1e6; timeWithVector = toc %Every time you call toc, it is stopped %Vector was ~200 times faster than the loop. This is typical %Function was ~30 times faster. %b) Checking whether elements are larger or smaller than some value A = rand(1e6,1); %Matrix A with a million random numbers from 0 to 1 clear B %clear B to be fair tic for ii = 1:length(A) %Go through all elements of A if A(ii,1) > 0.5 %Check if it is larger or smaller than reference value B(ii,1) = 1; %If larger, assign 1 to appropriate spot in B else B(ii,1) = 0; %Otherwise zero end end timeWithLoop = toc clear B tic B = A>0.5; %All at once timeWithCommand = toc clear B tic temp = find(A>0.5); %Use the find function to get the indices of the locations in A where the condition is true B(temp(:,1),1) = 1; %Use these indices in B, setting them 1. timeWithFind = toc %Find is an amazing function. It doesn't give you values, it gives you the %indices of the values where something you care about is true. %Command was ~60 times faster than the loop %Find was ~15 times faster than the loop
timeWithLoop =
0.84983
timeWithFunction =
0.011541
timeWithVector =
0.0017938
timeWithLoop =
1.4143
timeWithCommand =
0.00097717
timeWithFind =
0.016161
% c) Add only numbers in the vector that are large enough %Now we combine these functions A = rand(1e6,1); %Our random matrix with a million elements cumsum = 0; tic for ii = 1:length(A) %Go through all elements of A if A(ii,1) > 0.5 cumsum = cumsum + A(ii,1); end end cumsum timeWithLoop = toc %Version with find tic temp = find(A>0.5); %Just find the indices of those that are larger - ONE command, not a million cumsum = sum(A(temp)) %Using these indices timeWithFunctions = toc %No difference in sum, but the functional way is ~75 times faster. %Apart from speed, you can make sets nicely with vectors %For instance %Create a matrix of odd numbers from 1 to 100, their square roots and %squares in 50 columns and 3 rows without a loop format shortg %this avoids output in scientific notation n = 1:2:100; %Every other one is an odd number temp1 = sqrt(n); %Their square root temp2 = n.^2; %Their square, element-wise M = [n;temp1;temp2] %Stack the vectors to get a matrix
cumsum =
3.7502e+05
timeWithLoop =
0.99794
cumsum =
3.7502e+05
timeWithFunctions =
0.015579
M =
Columns 1 through 6
1 3 5 7 9 11
1 1.7321 2.2361 2.6458 3 3.3166
1 9 25 49 81 121
Columns 7 through 12
13 15 17 19 21 23
3.6056 3.873 4.1231 4.3589 4.5826 4.7958
169 225 289 361 441 529
Columns 13 through 18
25 27 29 31 33 35
5 5.1962 5.3852 5.5678 5.7446 5.9161
625 729 841 961 1089 1225
Columns 19 through 24
37 39 41 43 45 47
6.0828 6.245 6.4031 6.5574 6.7082 6.8557
1369 1521 1681 1849 2025 2209
Columns 25 through 30
49 51 53 55 57 59
7 7.1414 7.2801 7.4162 7.5498 7.6811
2401 2601 2809 3025 3249 3481
Columns 31 through 36
61 63 65 67 69 71
7.8102 7.9373 8.0623 8.1854 8.3066 8.4261
3721 3969 4225 4489 4761 5041
Columns 37 through 42
73 75 77 79 81 83
8.544 8.6603 8.775 8.8882 9 9.1104
5329 5625 5929 6241 6561 6889
Columns 43 through 48
85 87 89 91 93 95
9.2195 9.3274 9.434 9.5394 9.6437 9.7468
7225 7569 7921 8281 8649 9025
Columns 49 through 50
97 99
9.8489 9.9499
9409 9801