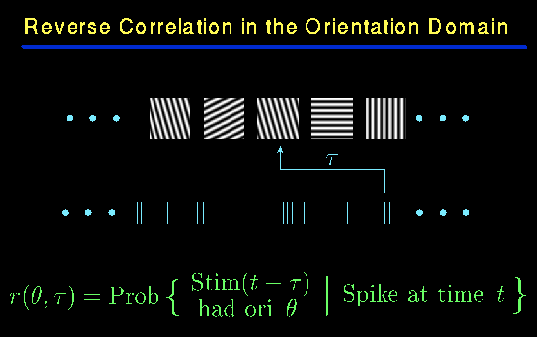
Abstract: Orientation tuning of neurons is one of the chief emergent characteristics of the primary visual cortex, V1. LGN cells that comprise the thalamic input to V1 are not orientation tuned, but the majority of V1 neurons are quite selective. Two main classes of theoretical models have been offered to explain orientation selectivity: feedforward models, in which inputs from spatially aligned LGN cells are summed together by one cortical neuron; and feedback models, in which an initial weak orientation bias due to convergent LGN input is greatly sharpened by intracortical feedback. To test these models we studied the dynamics of orientation tuning - how the orientation tuning of a neuron evolves with time - using a novel method: reverse correlation in the orientation domain. We find that the broad orientation tuning seen in the input layers 4C-alpha and 4C-beta is associated with very simple dynamics. However, sharper orientation tuning in supragranular and infragranular layers is accompanied by more intricate dynamical features, such as ``rebound'' responses, delayed secondary peaks, and sharpening of orientation tuning with time. Simulations of feedforward networks yield plain dynamic responses. In contrast, many of the dynamical features observed outside layer 4C arise naturally in feedback models. Therefore, our experimental results imply that the relatively broad orientation bias seen in 4C-alpha and 4C-beta may be computed by a feedforward network, but that cortical feedback is responsible for sharpening orientation-selectivity and causing intricate dynamical responses in macaque V1.
